Math Chick

Hands-On, Discovery Learning & Tech integration for Math, Science and STEM

Blog

Multiplying Fractions – When multiplying doesn’t lead to bigger products

One of the biggest mistakes we make as teachers is making generalizations about math and teaching our students about them. For instance, I have had kids tell me, “I know we are going to multiply in this problem because the answers are bigger”, or “I know we divide because the answer is smaller” or when students say “I have to always put the bigger number on top when we subtract” These statements have been taught to these students throughout their years.
In some instances these are correct statements, but they are generalizations that are not always true. Later on they will subtract a greater number from a smaller number resulting in a negative number. In my case I saw all of these generalizations when I taught sixth grade. As their teacher, I had to go back and change their thinking and prove to them that the generalizations were not always true and show examples as to when they were not true.
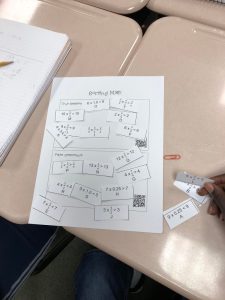
Multiplying fractions was one of the generalizations I had to conquer. In Texas, there is a standard that explicitly states for students to compare the product to the factors. This was a standard that I spent some time on even though it was a supporting standard. I feel like the supporting standards are just as important as the readiness standards because they lay the foundation for deeper, rigorous, and more meaningful operations.  I prepared an activity that allowed students to activate prior knowledge (from fifth grade) to construct new meaning and form a new generalization about multiplying and finding the products.
In fifth grade, students multiplied whole numbers by fractions and vice versa, using models and repeated addition. This laid the foundation for what the sixth graders would be exploring.  Students really took the time to analyze how the factors were related to the product.

* For instance, a whole number multiplied by a fraction less than one whole will result in a product that is less than the whole number factor used in the original problem.  5 x 1/4 < 5
* On the other hand, a whole number multiplied by a fraction more than a whole, will result in a product that is greater than the whole number factor used in the original problem. 5 x 6/4 > 5
* Finally, a whole number multiplied by a fraction equal to one whole will result in a product congruent or equal to the whole number used in the original problem.  5 x 4/4 = 5

Allowing students to fully explore these outcomes and come up with their own generalizations, gives students ownership for their own learning. Students came up with their own predictions and then tested those predictions and were validated with the results.

Students completed a sort while applying what they learned with a partner. This allows students to interpret what they have learned while applying it in a true or false situation. Students use QR codes to receive immediate feedback. Afterwards students completed a coloring sheet as homework/exit slip. 
You can get your hands on this activity, which includes, guided instruction and exploration, true/false sort and coloring sheet, right HERE on my TpT store. 
After this lesson we moved onto the algorithm for multiplying fractions.  This is a huge standard and could be a fraction times a fraction, fraction times a mixed or a mixed times a mixed. We used one of my free TpT games, called Super Six to help us practice! Students loved the game and you can get it for FREE!!! Right HERE! 
Here are some other products that worked wonders in my classroom to help me teach 6.3E Multiply and Divide Rational Numbers! 
Until next time! 
Peace, Love, Math

Integer Operations- From Chips to Number Lines and Beyond!

So this was my first time teaching integers, and I had to learn a lot! I relied on YouTube and watched videos on how to teach integer operations with chips and number lines. Our standards specifically say that students should recognize the models when adding, subtracting, multiplying or dividing integers. If you are anything like me or I guess I should say as old as me, you were taught the algorithm instead of how to perform the operation with a model. Why is a negative times a negative a positive? I had no clue, but I had been taught that, so that is what I did. So because of that, I needed to research how to show students the operation using a model and I am so happy that I did! This research helped me to understand the why behind integer operations so that I could teach my students the why behind the operations.
I modeled the operations with chips and number lines.  I only modeled the operation instead of teaching the students rules, algorithms or tricks.  I allowed the students to come up with those rules while working with the chips and number lines. Then as a class we tested their predictions and theories. Students came up to the document camera and led the class while completing examples.

After the students felt comfortable with using the chips and/or number line I assigned a stop motion project using Google Slides. Yep you read that right! Stop Motion Videos using Google Slides. I gave students directions and a rubric to create their own stop motion video. Here is the link to the PDF, for FREE! >>>>> Stop Motion Integer Project <<<<<<<
Here are a couple examples of students stop motion videos! They turned out amazing!
The students loved making these stop motion videos! Afterwards, we completed more activities centered around integer operations. These activities were awesome and can be found on my TpT store:
I especially loved the Digital Breakout! Have you used digital breakouts in your classroom yet? 
Until next time! 
Peace, Love and Math

Classifying Numbers into Rational, Integers and Whole Numbers TEKS 6.2A

This activity is FULLY aligned to TEKS 6.2A which is to classify numbers into rational, integers and whole numbers. 

The first thing I created was an interactive journal entry. I love to use interactive organizers in my math journals! I color coded the paper to make the graphic organizer pop once it was glued into the math journal. Each color stood for a different type of number. Before we organized the numbers into our sorting mat, we took notes on the definitions of each. Of course, I told students that there are irrational numbers in the world but they would encounter those later, not this year. 
Once the organizer was glued into the journal, students worked in partners to sort the numbers into rational, integer and whole. I asked the students not to glue in the numbers so that we could talk about each number to make sure all numbers are placed in the proper place before gluing. I gave them about 10 minutes to talk about the numbers and then we went over it as a whole group. 

Since this was my first time teaching this concept, I made higher level questions for me to ask the students.  This helped me to focus my thoughts and think about what I wanted to say prior to the lesson. I included these questions into the product that I uploaded to my Teachers Pay Teachers Store. 
The next day, as a formative assessment, I shared a Google Drawing with the students that they worked with a partner on to sort 33 numbers virtually. This was an awesome way to integrate technology and the kids could really discuss each number with their partners. 
I loved how this lesson came out and it worked well in my classroom. If you would like to try it in your classroom, here is the link to my TEKS 6.2A Classifying Numbers Activity. 
Until next time! 
Peace, Love, Math! 

Equivalent Equations and Properties of Equations

So my second week in 6th grade was a tough one! TEKS 6.7C and 6.7D are no joke! It may have been that I was so used to 5th grade standards that this one through me for a loop or it was just a hard concept. Either way, I had to develop a way to teach the concept to the kids and quite frankly, myself! So I developed an entire learning cycle to help us both!

We first explored equivalent equations using this sorting activity! It is free! And you can get your own copy here>>> Equivalent Equations Sort It also contains QR Codes!!!

Now to take those Math Properties!
First I used the 5 E model. For Engage and Explore- I always like to allow students to make sense of a concept by themselves and use me as a resource or facilitator. I developed posters to hang around the room. Students rotated around the room and tried to make sense of the math that was being presented in each poster. I gave students post-it notes and each set of partners wrote what they observed from these posters.

The students did really well, with their observations and were excited to learn the WHY? behind each property. 
Explain- I created a foldable that includes places for definitions, how to remember the term and an example. I made a pre-filled out version for myself so that I kept to the script, haha. The students related the foldable back to the posters they had visited earlier. Some students had A-Ha moments while others still needed some more direct instruction. 


Elaborate- Students looked at 24 equations and sorting them based on a property. Distributive, Commutative, Associative, Inverse, Identity and Non-Examples. I used Non-Examples so that students really look at each equation to make sure both sides are equal. You know me and I always include technology! So I made these cards with QR codes so that students receive immediate feedback.  

Evaluate- I created a google form with 10 questions. I used this as a quick check to form my small group instruction.  


Enrich- I developed an enrichment question so the students have the chance to analyze the math and then justify their response. Students completed this the next day for me and I was pleasantly surprised that they did really well with this topic! (and so did I ) 

Afterwards I realized that a through and developed lesson plan, will always help teach a harder topic! 

If you want to get your hands on all of the activities listed here, they can all be found in one download! Click Here >>>> Entire Learning Cycle on Math Operations 

Until next time!
Peace, Love, Math


Prime Factorization Fun!

I love to teach Prime Factorization! This year I have added a new activity into the mix! It was so much fun! The kids were engaged and worked through many rigorous problems to show their prime factorization skills. The activity is called Penny’s Prime Factorization Predicament.  This is an escape room type activity that allowed students to work out several problems to decipher clues which led to other clues hidden all around the school. The students absolutely loved it! The first clue was a coloring clue that led the students to find clue 2 in the cafeteria.

The next clue was using exponents and multiplication to determine the composite number.  This led the students to decode a secret message to reveal the location of the next clue, the nurses office. 
Once they received the next clue from the nurse, the students saw a QR code that led them to a Google Form. The Google form had a series of prime factorization problems that the students worked through, but if they answered incorrectly, the students had to sit through a video that explained the steps of prime factorization before answering the question again. 

At the end of the form the students knew where to go to find the next clue.  Students received the next clue which contained puzzle pieces. Students properly matched up the puzzle pieces then rearranged the pieces to reveal a word which led them to the next clue. 

The students final clue was to research a publishing date on a famous children’s book then find the prime factorization of that year. Students were allowed to research the book on their chromebooks. 

At the end, students received a congratulations letter from me 🙂 
I loved how engaged they were through out the entire activity! This was rigorous, relevant and exciting for the students and ME! If you would like to get your hands on this awesome activity click HERE! 
Before we spent the day on this activity, we practiced prime factorization by playing BINGO! 

You can also find the BINGO game HERE! 
Tune in next time when I tell about my Math Properties Activities! 
Peace, Love, Math
Jennifer

Top 5 Back to School Tips to Keep Your Sanity! Plus a Giveaway!

It is that time again, where we lose sleep over cute classrooms, professional development and engaging activities.  This will be my 15th year of teaching and I am still up early worrying about stuff that I need to do! I will be presenting to the new teachers at my school today and I have come up with 5 Back to School tips to KEEP YOUR SANITY!

1. Cute Classrooms take time, especially if you are a new teacher, and won’t get paid until the end of September ( I remember this time )! Just do what you can do, to make it cute.  Don’t get caught up in Instagram and Facebook photos of cute and perfect classrooms.  Those classrooms took time and years to put together.  Your students will love you based on the relationship you form with them, not because you have the cutest classroom ever. Super Tip– Use fabric for your bulletin boards.  The fabric wont fade and will last for years! Plus you can buy fabric that has an awesome theme, print or design to make your boards POP!

2.  You are NOT ALONE! The first couple of weeks are stressful for EVERYONE regardless of how long they have been teaching. Make sure to breathe, relax when you get home and remember you are not the only one who feels stress. Super Tip- Form a relationship with your team.  I am so lucky to work with my best friends! I could not imagine going through a school year without them.  We share our feelings and have each other’s back.

3. Set expectations and rules the minute the students come into the class.  Once you have set those expectations and rules for the class, be consistent and vigilant. This will be stressful in the beginning and you will sound like a parrot, just repeating yourself, but after a month or two (may be a semester) the students will get it and then you will not have to repeat yourself anymore. Super Tip– Have students create the rules with you.  You can facilitate the discussion and lead students towards the rules you want. The students will have more buy in when they are a part of the process.

4. Everyday is a new day and learn from your mistakes! There will be days that your lesson doesn’t go the way it was supposed to, or there are drills or assemblies in the middle of instruction or you spill coffee all over your cute outfit.  Those days suck but the good thing about those sucky days is that they are over the minute your head hits the pillow.  You wake up and guess what? It is a new day! Leave the mistakes behind you, learn from the mistakes and move forward.  Super Tip- Have this same belief about your students.  Kids have bad days too.  Don’t hold a grudge.  Kids make mistakes so let them know that tomorrow is a new day and a clean slate.

5. Prepare in advance! Know your content and standards! If it is your first year, you may want to plan out what you want to say and do each day.  You never want to “wing it” because the kids will know and they will not be engaged.  You want to prepare and anticipate everything that can go wrong with an activity.  Super Tip- Find someone who does know their content and use them as a resource.

I am grateful to be a part of an amazing giveaway! So let’s celebrate the start of the new school year by winning some FREE GIFT CARDS!!!! 3 winners will be chosen!

a Rafflecopter giveaway

I’m Moving On Up! (To Sixth Grade That Is :)

Next year I will be looping to sixth grade math.  I am very excited about the change.  I will be headed back down to fifth after next year so please bare with me fellow fifth grade teachers, I will be back! I am looking forward to the challenge and can’t wait to share my lessons and activities with you all! If you can, please forward my blog to your sixth grade teachers, I would love to collaborate! I am currently working on an escape room challenge for prime factorization and a complete learning cycle for teaching the properties of math operations.

To help celebrate all the wonderful things in life right now, #hellosummer, #hellosixthgrade, #hellovacay, I have joined in with other wonderful teachers to offer an amazing giveaway!

Who doesn’t love a good giveaway?? The raffle begins Friday, June 23rd and ends at midnight on Saturday, July 1st. The more links you visit and follow the more chances you have to win! There are 2—$100 TpT Cards to win and 1—$50 TpT Card to win!

GIVEAWAY IS CLOSED

In addition to the wonderful giveaway, we will be featuring products up to half off! Just go to TpT and search #hellosummer to find amazing deals! This hashtag sale will be from June 23rd through June 25th.

Thank you all for following Math Chick! I hope you continue to follow now that I am moving to 6th grade! Share the wealth with your fellow math teachers 🙂

Until next time,
Peace, Love, Math
Jennifer

Amazing Augmented Reality in the Classroom! (An Alternative to QR Codes)

I am SUPER excited about this newest technology that I have integrated into my math class! I am sure you have seen Pokemon Go and how it uses Augmented Reality or AR to bring to life Pokemon in a game style platform.  What I have done is take this AR technology and I have made task cards that come to life!
For years, we have used QR codes to provide students with immediate feedback and as a way to integrate technology into the curriculum.  I wanted to find a new and fresh way to offer students that same feedback but by using a different platform. Here is where Aurasma hits the scene!

Aurasma is a free app that is available on android tablets as well as iPads.

Aurasma allows students to scan a picture or task card and then watch in real time, the picture or task card, come to life! Students are so excited to see this technology in action! I have made a sample pack of task cards that you can access HERE. You can try the task cards and technology for FREE! Once you see the technology in action, you may never want to go back to QR Codes!
Here is a breakdown on how to use the cards!
1. Download the free Aurasma App on the device you will be using.
2. In order to make the task cards come to life, you must follow my Aurasma channel.  You can scan this QR Code to access and follow my channel or you can use this link https://auras.ma/s/xh2IN
3. Once you have the app and have followed my channel, you are ready to access the content on my task cards.
4. Open the app and start scanning the task cards much like a QR code.
I love this technology! You could also use this in several ways! I personally have thought about “Student of the Week”.  Students could scan a picture of the “Student of the Week” and it would reveal a short video that the student of the week has made about him/herself!  This same thing could be done with “Meet the Teacher Night”.  Parents could scan a picture of the teacher and watch a video that tells all about the classroom and teacher.
Students could create their own Aurasmas by taking a picture of their work and making it come to life by retelling a little bit about the content.
Another AR or Augmented Realty app that is absolutely breathtaking is Quiver!
Quiver is a free app available on iPads or android devices.  In order to use this technology, you will need to print off Quiver sheets to use.  There are several free Quiver sheets to use, and some sheets that cost money.  I printed off the free sheets and we used them in class at the end of the year.  Students absolutely loved them! To access the coloring sheets click here: https://www.quivervision.com/coloring-packs/
I would love to see more sheets become available on Quiver because it is AMAZING! Using the sheets you can see a volcano come to life, you can color a beetle and watch it come to life and then learn about the parts of an insect, you can color the world and then literally have the world at your fingertips! I wouldn’t mind spending a little money in order to get quality sheets to use with this app.
I am hooked on Augmented Reality in the classroom! I can’t wait to find more ways to use the technology in class.  I would love to hear how you have used Augmented Reality in your classroom, feel free to share in the comments below.
Peace, Love, Math-
Jennifer

Digital STEM Challenge Activity- How Much Water Can A Penny Hold?

I love to do STEM challenges! I have always wanted to integrate more technology into my STEM challenges but hadn’t fully wrapped my brain around how to integrate it properly.  I have done many digital interactive lessons for math class so I decided to try to take a STEM challenge I already had created and turn it into a digital STEM challenge!

The result: AMAZING!!! Not only were the students able to have a hands-on experience with a science and math challenge but they were able to practice making tables, graphs and typing in text boxes.  These students are learning 21 century skills in a meaningful, real world way!

Afterwards students designed their own investigation.  Students could compare the number of water droplets on pennies and nickels or the water droplets on clean pennies versus dirty pennies.  Students could think of what ever they wanted to test! Students loved designing their own investigation!
I am very happy with how this turned out! I will be making two more digital STEM challenges, so stay connected! If you want to get your hands on this digital challenge check it out in my TpT Store or press this LINK! 
Until then-
Peace, Love and Math
Jennifer

Let’s Celebrate! STAAR Scores are Back!

What a perfect time to celebrate! 
Let me start by saying, I believe that test scores do not define a child in his or her entirety. My students have grown so much and showed that growth on this STAAR test. With or without a test, EVERY student has grown this year, and EVERY student has evolved into a better reader, mathematician, and scientist. I strongly feel that this is the reason they are able to perform so well on the tests. Not because they have been taught how to do a test, but have learned and discovered their inner mathematician, scientist or reader and can think critically about the material.

I am very excited to announce that we received our test scores for Math and Reading STAAR tests.
I wanted to share with you just how amazing your students are! 
I had 100% of my students (every student including those who has special education support and accommodations) passed the first administration of the STAAR test! I am very proud of them and all of their hard work! 

Just in time to help me celebrate is a TEACHER GIVEAWAY!  I have joined in on Teacher Genie’s amazing celebration! Way to go! 4000 members is AWESOME! 


GIVEAWAY IS CLOSED!

Raffle Ends April 28th @ 12am
GOOD LUCK!!!!!

Peace, Love and Math!
Jennifer

↑ Top of Page